我想你大概不是来找定义的,我就说我对这玩意几何上的理解。
微分总体是为了刻画函数局部的增长率,高中的导数就是斜率,那语境到多元函数的时候,我们怎么办?
z如果是一个三维里的曲面,当某一个点可微的时候,我们怎么刻画这玩意的局部增长率?
回想导数的定义:
![[公式]](https://www.zhihu.com/equation?tex=f%27%28x_0%29%3D%5Clim_%7B%5CDelta+x+%5Cto+0%7D%5Cfrac%7B%5CDelta+y%7D%7B%5CDelta+x%7D%3D%5Cfrac%7Bdy%7D%7Bdx%7D)
这其实是在x0这个点附近找另一个f上的点,连起来,用y的变化量除以x的变化量这个代表这一部分的斜率,之后使两点不断靠近(取极限),作为一个点的定义,也就是斜率。这个过程就是所谓的线性逼近(用直线逼近嘛,很写实了。。)
那当我们处理多元函数怎么办?
拿二元函数z(x,y)举例好了,我们还想复制上面的过程。考察z(x0,y0)变成z(x0+h,y0+h)的变化量,定义出多元函数的类似导数的东西。
但是由于我们对多元函数缺乏‘斜率’这样直观好用的几何对象(不信你可以试一试画一个直三棱锥,想想怎么表示这个你需要的‘斜率’),所以我们先想办法考察我们会的东西:
把(x0,y0)的y轴固定下来,这样相当于把二元函数z在y=y0这里切出了一个切面,这样我们就可以把切面上的这条曲线(当然这条曲线也属于z)拿来算导数了:
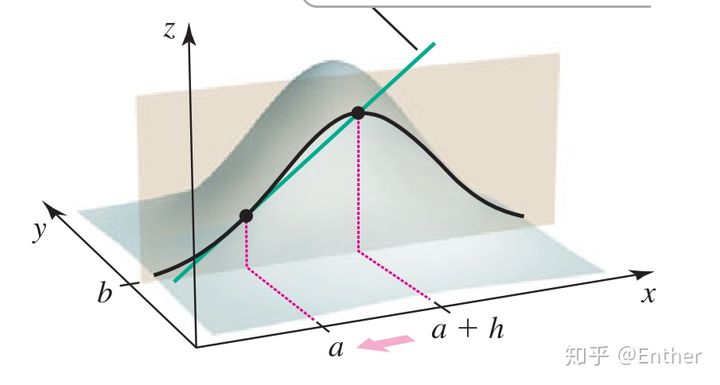 图片来自香港科技大学Frederick Tsz-Ho Fong老师的lecture notes
图片来自香港科技大学Frederick Tsz-Ho Fong老师的lecture notes
因为固定了y,我们把这叫做z在x方向上的偏导数:
![[公式]](https://www.zhihu.com/equation?tex=%5Cfrac%7B%5Cpartial+f%7D%7B%5Cpartial%7Bx%7D%7D+%3D%5Clim_%7Bh+%5Cto+0%7D%5Cfrac%7Bf%28x%2Bh%2Cy%29-f%28x%2Cy%29%7D%7Bh%7D) ,类似的,我们很容易得到关于y的偏导数。
,类似的,我们很容易得到关于y的偏导数。
从这里出发,我们再次利用线性逼近的思想,并推广一步:
当我们考察的函数“邻域”足够小的时候,我们可以把曲面当成平面。这就是所谓线性近似的几何解释。注意是解释,不是证明,不是定义。完整的定义,我们需要借助链式法则,或(过时又被抛弃的)高阶无穷小量给出。
得到全微分的定义(二元):
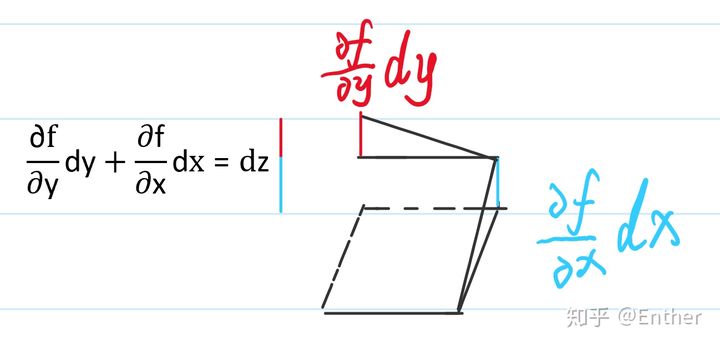 这个可不是证明哦
这个可不是证明哦
如果你喜欢代数证明的话,全微分是链式法则的直接结果。
是不是觉得还缺些什么?之前说偏微分的时候把偏微分定义在曲面切平面上,不就可以定义更加自然的多元函数”导数“了吗?事实上这就是所谓的方向导数,也就是任意某个方向的偏导数。如果想进一步了解,请找梯度与方向导数。