浅谈变分原理

吃老本的物理教师、民科老咸鱼

对付数学物理中极值问题，变分大法（variational principle）可谓是杀人放火居家旅行的必备工具。今天这篇就来介绍变分法的基本思想。

碎碎念：我一个教物理的，为啥成天一个劲写数学呢？？？

变分大法轶事

大约1696年的6月，瑞士数学家 Johann Bernoulli 在 Acta Eruditorum（第一份德语的科学期刊）上向全世界的数学家发起了一项挑战。他提出了这么一个数学问题：让一个物体从静止开始沿着一个光滑无摩擦的轨道下滑，如果要求下滑过程耗时最短，轨道应该是什么形状？（在这篇文章后面的举例中，我们会来具体处理这个问题）

盗图来自新浪围脖，具体出处不明 / 更新：谢评论区 Nick Choi 指出，动图出自油管播主 Vsauce，链接在：https://youtu.be/skvnj67YGmw

这个问题被称作最速降曲线问题（the brachistochrone problem）。这个问题是如此有趣，吸引了很多数学家的关注。Johann 本人利用光学原理类比给出了一种解法，他更牛掰的哥哥 Jacob Bernoulli 想到了另一种解法（是的，Bernoulli 家族盛产数学家，走量的那种）。此外，大名鼎鼎的 Gottfried Leibniz（跟牛顿争微积分发明权的那位），Guillaume de l'Hôpital（洛必达法则就是他的名号）等人都给出了各自的解法。

风声不久后也传到了科学界早已功成名就的 Issac Newton 耳里。1697年1月的某天，牛爵爷此时已在皇家造币厂任职，他开开心心下班回家，发现了来自 Johann Bernoulli 的挑战书。牛爵爷可能有点不太开心，内心也嘀咕着：老子牛逼顿，你们这些外国佬少来跟我在数学问题上嚣张！或者按他自己的原话：I do not love to be pestered and teased by foreigners about mathematical things. 于是牛爵爷也忍不住试了试水。以牛爵爷的智商，他大概也就经过了那么一晚上的思考，就运用变分法解决了问题，转手就写了封信寄回给了 Johann。

不过 Newton 很低调地将他的解答匿名寄了回去。然而 Newton 的解法是如此之风流潇洒，令人拍案叫绝，即便没有署名，Johann 也很快意识到了真正的作者是何方神圣。对此，他做出了著名的评价：I recognize the lion by his claw mark.

其实早在10多年前，牛爵爷在考虑在流体中会受到最小阻力的旋转曲面该是什么形状的问题时，已经构建起了变分原理的基本思想。经过一大批数学家的杰出工作，现在变分法已经成为了数学分析中的求极值问题的一种重要方法。

故事说这么多，我们下面就要来开始硬核的讨论了。

变分大法

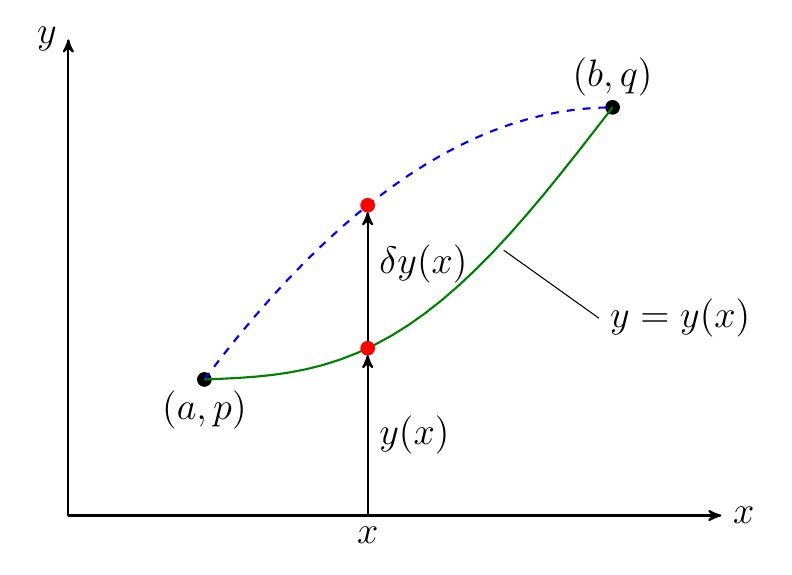
假设我们有两个定点 $(a,p)$ 和 $(b,q)$ ，连接这两点的任意曲线的方程 $y = y(x)$ 都将满足如下的边界条件：

$y(a)=p, \quad y(b)=q \quad (1) \\$

现在考虑如下形式的定积分：

$I = \int_a^b f(y,y')\mathrm{d}x \quad (2) \\$

其中 $f(y,y')$ 是关于 $y(x)$ 和其一阶导数 $y'(x)$ 的函数，我们期望找到一个具体的 $y(x)$ ，使得 $I$ 有极值（极大或极小）。

注意在一般的极值问题中，我们考察的是自变量 $x$ 的变化： $x$ 取值多少时，函数会有极值。而现在这个新问题的不同之处，我们考察的是函数 $y(x)$ 的变化： $y(x)$ 是什么形式时， $I$ 会有极值（高大上叫法： $I$ 称作函数 $y(x)$ 的泛函）。然而这两类问题依然有共通之处：当 $I$ 取极值时，对 $y(x)$ 作微小的变化， $I$ 在一级近似下应该保持不变。

如果 $y(x)$ 有微小改变 $\delta y(x)$ （高大上叫法： $\delta y(x)$ 称作函数 $y(x)$ 的变分），那么 $f(y,y')$ 的变化为：

$\delta f = \frac{\partial f}{\partial y}\delta y + \frac{\partial f}{\partial y'}\delta y' \quad (3) \\$

$I$ 相应的变化为：

$\delta I = \int_a^b \left[ \frac{\partial f}{\partial y}\delta y + \frac{\partial f}{\partial y'}\delta y' \right] \mathrm{d}x \quad (4) \\$

方括号里的第二项可以改写成 $\frac{\partial f}{\partial y'} \frac{\mathrm{d}(\delta y)}{\mathrm{d}x}$ ，然后我们可以进行分部积分

$\begin{aligned} \int_a^b \frac{\partial f}{\partial y'}\delta y' \mathrm{d}x & = \int_a^b \frac{\partial f}{\partial y'} \mathrm{d}(\delta y) \\ & = \frac{\partial f}{\partial y'} \delta y \Bigg|_a^b - \int_a^b \delta y \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{\partial f}{\partial y'} \right) \mathrm{d}x \end{aligned} \\$

由于 $y(x)$ 的边界条件固定， $\delta y(a) = \delta y(b) = 0$ ，所以分部积分出来的第一项为零，仅第二项有贡献。代回（4）式中，稍作化简可以得到

$\delta I = \int_a^b \left[ \frac{\partial f}{\partial y} - \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{\partial f}{\partial y'} \right)\right] \delta y(x) \mathrm{d}x \quad (5) \\$

如果 $I$ 有极值，对任意满足边界条件的 $\delta y(x)$ 都必须有 $\delta I = 0$ ，这就要求：

$\boxed { \frac{\partial f}{\partial y} - \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{\partial f}{\partial y'} \right) = 0 } \qquad (6) \\$

这便是传说中的 Euler-Lagrange 方程，它是变分法的核心定理。有了此等大杀器，原则上就可以找出所寻求的极值函数 $y(x)$ 。

通常来讲 Euler-Lagrange 方程会是一个二阶的微分方程， $y(x)$ 的通解中含有的两个待定常数刚好可以通过两个边界条件确定。我们下面来举几个例子操练操练。

例1：两点间的最短路经

先来一个简单的例子小试牛刀。

给定平面上两点 $(a,p)$ 和 $(b,q)$ ，连接它们的长度最短的曲线是什么？

这个问题的答案小学生都知道，我们在这里用变分法来杀杀这只小鸡仔。

曲线 $y(x)$ 上相近的两点 $(x,y)$ 和 $(x+\mathrm{d}x,y+\mathrm{d}y)$ 之间的曲线元长度为：

$\mathrm{d}s = \sqrt{\mathrm{d}x^2 + \mathrm{d}y^2} = \sqrt{1+y'^2} \mathrm{d}x \qquad (7) \\$

曲线的总长度为：

$S = \int_a^b \sqrt{1+y'^2} \mathrm{d}x \qquad (8) \\$

现在希望 $S$ 有最小值，我们可以取 $f(y,y') = \sqrt{1+y'^2}$ ，运用 Euler-Lagrange 方程来寻找可以让 $S$ 有极小的函数 $y(x)$ 。注意到

$\frac{\partial f}{\partial y} = 0, \qquad \frac{\partial f}{\partial y'}=\frac{y'}{\sqrt{1+y'^2}} \\$

代回（6）式中，容易得到

$\frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{y'}{\sqrt{1+y'^2}} \right) = 0 \qquad (9) \\$

括号里这一大坨的导数为零，那么括号里这一大坨必然是一个常数，我们马上可以推出 $y'$ 也必然是一个常数。因此我们需要寻找的 $y(x)$ 满足直线方程：

$y = kx + c \qquad (10) \\$

斜率 $k$ 和截距 $c$ 很容易通过边界点的坐标算出。由此我们证明了大家非常熟悉的结论：两点之间直线段的距离最短。

例2：最速降曲线

问题在开篇的历史故事介绍中已经有提到，我们这里直接进入解答环节。

为方便起见，我们将坐标系的 $y$ -轴搞成朝下的方向，斜向下的轨道可以由函数 $y(x)$ 给出，其中轨道的起点和终点分别设为 $(0,0)$ 和 $(a,b)$ ，我们来试求最速降曲线的函数式。

当物理下滑到 $(x,y)$ 位置时，它的速度大小可以根据能量守恒关系解出

$\frac{1}{2}mv^2 = mgy \qquad \\ v=\sqrt{2gy} \qquad (11) \\$

而根据定义，速度大小等于单位时间内走过的轨道长度

$v = \frac{\mathrm{d}s}{\mathrm{d}t} = \sqrt{1+y'^2} \frac{\mathrm{d}x}{\mathrm{d}t} \qquad (12) \\$

其中我们已经利用了之前（7）式中得到的结果。

（11）与（12）式联立，可以写出：

$\mathrm{d} t = \sqrt{\frac{1+y'^2}{2gy}}\mathrm{d}x \qquad (13) \\$

积分后就可以得到总时间的表达式：

$T = \frac{1}{\sqrt{2g}} \int_0^a \sqrt{\frac{1+y'^2}{y}}\mathrm{d}x \qquad (13) \\$

为了找出让 $T$ 取得极小的 $y(x)$ ，我们可以取 $f(y,y') = \sqrt{\frac{1+y'^2}{y}}$ ，再套用 Euler-Lagrange 方程来怒算一波。

$\frac{\partial f}{\partial y} = -\frac{1}{2} \sqrt{\frac{1+y'^2}{y^3}}, \qquad \frac{\partial f}{\partial y'}=\frac{y'}{\sqrt{y(1+y'^2)}} \\$

丢回（6）式里面，我们可以得到这么一个初步的方程：

$\frac{1}{2} \sqrt{\frac{1+y'^2}{y^3}} + \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{y'}{\sqrt{y(1+y'^2)}} \right) = 0 \qquad (14) \\$

看到这种东西，要保持平静，铁了头往下算，要相信好多恶心的东西会神奇地同归于尽。

$\frac{1}{2} \sqrt{\frac{1+y'^2}{y^3}} + \frac{y''}{\sqrt{y(1+y'^2)}} -\frac{1}{2} \frac{y'^2}{\sqrt{y^3(1+y'^2)}} - \frac{y'^2y''}{\sqrt{y(1+y'^2)^3}} = 0 \qquad \\\frac{1}{2}(1+y'^2)^2 + y(1+y'^2)y'' - \frac{1}{2}y'^2(1+y'^2) - yy'^2y'' = 0 \qquad \\\frac{1}{2}(1+y'^2) +yy''=0 \qquad (15) \\$

瞧，柳暗花明又一村。不过这还远没完，解这个二阶微分方程还需要一个骚操作。我们对上式乘上一个 $2y'$ ：

$y' (1+y'^2) +2yy'y''=0 \qquad \\ \frac{\mathrm{d}}{\mathrm{d}x} \Big[ y(1+y'^2) \Big] = 0 \qquad (16) \\$

感谢 CCAV 这玩意儿居然是个全微分，它要等于零，方括号里那一坨等于常数就完儿事了。且让我们将这个常数写作 $k$

$y(1+y'^2) = k \qquad \\ y'^2 = \frac{k}{y} - 1 = \frac{k-y}{y} \qquad \\ y' = \frac{\mathrm{d}y}{\mathrm{d}x} = \sqrt{ \frac{k-y}{y} } \quad (17) \\$

原来的二阶微分方程降次变成了一阶，我们终于可以愉快地分离变量两边积分了

$x = \int \mathrm{d}x = \int \sqrt{ \frac{y}{k-y} } \mathrm{d}y \qquad (18) \\$

作三角换元，设 $y = k\sin^2 \theta$ ，则

$x = \int \sqrt{ \frac{k\sin^2\theta}{k-k\sin^2\theta} } \mathrm{d}(k\sin^2\theta) \qquad \\ x = \int \frac{\sin\theta}{\cos\theta}2k\sin\theta\cos\theta\mathrm{d}\theta \qquad \\ x = \int 2k\sin^2\theta\mathrm{d}\theta = k\int (1-\cos2\theta)\mathrm{d}\theta \qquad \\ x = k\theta -\frac{1}{2}k\sin2\theta + c \qquad (19) \\$

其中 $c$ 是积分常数。我们再作逆变换变回到 $y$ ，注意到 $\sin\theta = \sqrt{\frac{y}{k}}$ ，于是

$\sin 2\theta = 2\sin\theta\cos\theta = 2 \sqrt{\frac{y}{k}} \sqrt{\frac{k-y}{k}} \\$

我们可以得到所求的最速降轨道的函数表达式：

$x(y) = k\sin^{-1} \sqrt{\frac{y}{k}} - \sqrt{y(k-y)} + c \qquad (20') \\$

轨道起点为 $(0,0)$ ，很容易得出 $c=0$ ，于是结果可以进一步简化

$x(y) = k \sin^{-1} \sqrt{\frac{y}{k}} - \sqrt{y(k-y)} \qquad (20) \\$

另一方面，轨道终点为 $(a,b)$ ，上面的常数 $k$ 还必须满足：

$k \sin^{-1} \sqrt{\frac{b}{k}} - \sqrt{b(k-b)} =a \qquad (21) \\$

可以证明，满足边界条件（21）的最速降曲线（20）将是一条摆线（cycloid）：它是圆周上的一个定点在圆沿直线滚动时所形成的轨迹。

从（20）式很难看出这个结论，但其实满足（17）式的 $y(x)$ 还可以写成如下的参数方程：

$x(\alpha) = R(\alpha - \sin\alpha), \qquad y(\alpha)=R(1-\cos\alpha) \qquad (22) \\$

其中 $R = \frac{1}{2}k$ 给出了滚动的圆的半径。可以作如下的验算：

$\frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\frac{\mathrm{d}y}{\mathrm{d}\alpha}}{\frac{\mathrm{d}x}{\mathrm{d}\alpha}} = \frac{\sin\alpha}{1-\cos\alpha} = \frac{\sqrt{1-\cos^2\alpha}}{1-\cos\alpha} = \sqrt{\frac{1+\cos\alpha}{1-\cos\alpha}} \\ \sqrt{ \frac{k-y}{y} } = \sqrt{ \frac{k - \frac{1}{2}k(1-\cos\alpha)}{\frac{1}{2}k(1-\cos\alpha)}} = \sqrt{\frac{1+\cos\alpha}{1-\cos\alpha}} \\$

这验证了（22）式的参数方程确实是（17）式的解。而参数方程可以更明确地表达出摆线的几何意义（如图）。

例3：悬链线

这个数学问题同样也起源于物理：悬在等高的两点间的受重力作用的软绳形成的曲线应该是什么形状？

这类曲线统称为悬链线（catenary ），在工程和设计中有广泛的应用。比如悬索桥、架空电缆等都会出现悬链线的设计，而在很多拱门、教堂拱顶的设计中，还会出现倒悬链线的踪影。

我们在此考虑一个稍有不同的问题。假设有等高的两个支点，它们的坐标为 $(L, h)$ 和 $(-L,h)$ 。软绳搭在这两个支点上，一部分悬在两个支点之间，多出来的部分自由下垂耷拉到地面上（如图所示）。

整个体系会自发去向势能最低的状态，因此我们需要找的便是势能最低状态随对应的 $y(x)$ 函数。

记软绳单位长度的质量为 $\rho$ ，并取地面高度为重力势能的零点。左右竖着的两段的质量均为 $\rho h$ ，重心在 $\frac{h}{2}$ 的高度，因此它们具有的重力势能为

$2\times (\rho h) g \frac{h}{2} = \rho gh^2 \qquad (23) \\$

至于悬挂在两个支点间的部分，我们可以先写出 $(x,y)$ 和 $(x+\mathrm{d}x,y+\mathrm{d}y)$ 之间一小段的重力势能：

$(\rho \mathrm{d}s) g y = \rho g y \sqrt{1+y'^2}\mathrm{d}x \\$

弯曲悬挂着的部分的总的重力势能就是

$\int_{-L}^L \rho g y \sqrt{1+y'^2} \mathrm{d}x \qquad (24) \\$

结合（23）与（24）式，整个体系的总势能为：

$V = \rho g \int_{-L}^L y \sqrt{1+y'^2} \mathrm{d}x + \rho g h^2 \qquad (25) \\$

注意到 $\rho g h^2$ 为常数，因此可以取 $f(y,y') = y \sqrt{1+y'^2}$ ，再套用 Euler-Lagrange 方程来找出让 $V$ 取得极小的 $y(x)$ 。

$\frac{\partial f}{\partial y} = \sqrt{1+y'^2}, \qquad \frac{\partial f}{\partial y'}=\frac{yy'}{\sqrt{1+y'^2}} \\$

代回（6）式中，可以先写出

$\sqrt{1+y'^2} - \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{yy'}{\sqrt{1+y'^2}} \right) = 0 \qquad (26) \\$

不要慌，要继续相信硬肝一波还是可以看到柳暗花明

$\sqrt{1+y'^2}-\frac{y'^2}{\sqrt{1+y'^2}}-\frac{y y''}{\sqrt{1+y'^2}}+\frac{yy'^2 y''}{\sqrt{(1+y'^2)^3}}=0 \\(1+y'^2)^2 - y'^2(1+y'^2) - yy''(1+y'^2) + y y'^2 y'' = 0 \\1+2y'^2+y'^4-y'^2-y'^4-yy''-yy'^2y''+yy'^2y'' = 0 \\(1+y'^2) - yy'' =0 \\$

似乎看起来也还可以接受？接下来依然一步骚操作，两边同乘以 $\frac{y'}{\sqrt{(1+y'^2)^3}}$ ：

$\frac{y'}{\sqrt{1+y'^2}} - \frac{y y' y''}{\sqrt{(1+y'^2)^3}} = 0 \qquad \\\frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{y}{\sqrt{1+y'^2}} \right) = 0 \qquad (27) \\$

再次神奇地化成了一个全微分，它要等于零，需要圆括号里那一坨等于常数。

$\frac{y}{\sqrt{1+y'^2}} = c \qquad \\y' = \frac{\mathrm{d}y}{\mathrm{d}x} = \sqrt{\frac{y^2}{c^2} - 1} \qquad (28) \\$

这问题又简化成了一个一阶的微分方程。常规操作，分离变量再两边积分：

$\mathrm{d}x = \frac{\mathrm{d}y}{\sqrt{\frac{y^2}{c^2} - 1}} \qquad \\x = \int \frac{\mathrm{d}y}{\sqrt{\frac{y^2}{c^2} - 1}} \qquad (29) \\$

不难想到用双曲换元，令 $y=c\cosh t$ ，于是 $\mathrm{d}y = c \sinh t$ ， $\sqrt{\frac{y^2}{c^2} - 1} = \sinh t$ 。（29）式变成

$x = \int c\mathrm{d}t = ct + d \qquad (30) \\$

其中 $d$ 为积分常数，它连同常数 $c$ 都必须匹配边界条件。

（30）式可以改写成 $t = \frac{x-d}{c}$ ，我们可以反解出 $y(x)$ 的函数式：

$y(x) = c\cosh\frac{x-d}{c} \qquad (31') \\$

在我们的问题中， $y(x)$ 显然关于 $y$ -轴对称，所以 $d=0$ 。因此

$y(x) = c\cosh \frac{x}{c} \qquad (31) \\$

支点坐标为 $(\pm L, h)$ ，因此边界条件还要求：

$h = c\cosh \frac{L}{c} \qquad (32) \\$

于是悬在两个支点之间的软绳的形态将有（31）式的双曲函数给出，其中的参数 $c$ 需满足（32）式的条件。

我们还可以试着讨论一下（32）式在什么情况下有解。令 $u = \frac{L}{c}$ ，或 $c = \frac{L}{u}$ ，则（32）式可以改写成

$\frac{h}{L} u = \cosh u \\$

作出图像，左边对应一条过原点、斜率为 $\frac{h}{L}$ 的直线，右边对应一条过 $(0,1)$ 后斜率快速增长的曲线。

可以想见，如果 $\frac{h}{L}$ 太小，方程将没有解。这时，相比支点的高度，支点之间悬着好长一段绳子，两侧荡着的部分提供的拉力根本拽不住中间那一大段的重量。而如果 $\frac{h}{L}$ 足够大，方程将有两个解，其中一个会对应稳定平衡，另一个对应非稳定平衡。可以证明较大的 $c$ 解会给出稳定平衡。

其他好玩的东西

烤羚羊：续浅谈变分原理：运动常数、拉格朗日乘子法zhuanlan.zhihu.com

未完待更

参考资料

Michael Stone & Paul Goldbart, Mathematics for Physics [Chapter 1: Calculus of variations]
Tom W.B. Kibble & Frank H. Berkshire, Classical Mechanics (5th Edition) [Chapter 3.6 The Calculus of Variations]
https://en.wikipedia.org/wiki/Cycloid
https://en.wikipedia.org/wiki/Catenary
https://en.wikipedia.org/wiki/Brachistochrone_curve