那些年遇到的无量纲数

• 雷诺数（Re）
• 努塞尔数（Nu）
• 普朗特数（Pr）
• 毕渥数（Bi）
• 傅里叶数（Fo）
• 马赫数（Ma）

01—雷诺数（Re）

英国物理学家老雷（雷诺）进行了大量的实验，并在1883年发表的报告中提出：自然界的流体流动有两种不同的流态，低速下为层流，流速增大后，流体流动过度为湍流（紊流）；在层流下流体的流动是有规则有秩序的，在湍流情况下，流体的运动是杂乱无章的。雷诺在大量实验的基础上，用所有影响流动状态因素的一个无因次组合数（雷诺数），来判断流动是层流还是湍流，定义为：

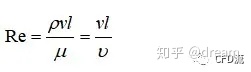
其中，ρ为流体密度，v为流体速度，l为特征长度，μ为动力粘度，υ为运动粘度

在工程实际中，一般当Re≤2000，认为管内的流动为层流；当Re>2000时，认为管内流动为湍流。

雷诺数实际上表征的是：惯性力和粘性力之比。当雷诺数较小时，流场中粘性力起主导作用，惯性力起次要作用；当雷诺数较大时，流场中惯性力起主导作用，粘性力起次要作用。

02—努塞尔数（Nu）

努塞尔数（Nusselt number），以德国物理学家威廉·努塞尔特（Wilhelm Nusselt）的名字命名，以纪念其对此方面研究的突破。努赛尔数的物理意义为是表示对流换热强烈程度的一个无量纲数。

其中，h为流体的对流传热系数，l为传热面的几何特征长度，k为流体的导热系数。

03—普朗特数（Pr）

普朗特数是流体力学中表征流体流动中动量交换与热交换相对重要性的一个无量纲参数，表明温度边界层和流动边界层的关系，反映流体物理性质对对流传热过程的影响。记为Pr。

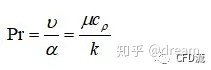
υ为运动粘度，α为热扩散系数，μ为动力粘度，c_ρ为比热容，k为导热系数。

当几何尺寸和流速一定时，流体粘度大，流动边界层厚度也大；流体导温系数大，温度传递速度快，温度边界层厚度发展得快,使温度边界层厚度增加。因此，普朗特数的大小可直接用来衡量两种边界层厚度的比值。

04—毕渥数（Bi）

表征固体内部单位导热面积上的导热热阻（内部热阻）与单位面积上的换热热阻（即外部热阻）之比。

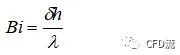
б是特征长度，h是表面传热系数，λ是导热系数。

Bi数越小，意味着内热阻越小或外热阻越大；Bi越大，意味着内热阻越大或外热阻越小。

05—傅里叶数（Fo）

傅里叶数可以理解为两个时间间隔相除所得的无量纲时间。

τ是从边界上开始发生热扰动的时刻起到所计算时刻为止的时间间隔，分母可以视为使边界上发生的有限大小的热扰动穿过一定厚度的固体扩散到l_c的面积上所需的时间。因此，Fo数可以看成是表征非稳态过程进行深度的无量纲时间。在非稳态导热过程中，这一无量纲时间越大，热扰动就越深入的传播到物体内部，因而物体内各点的温度越接近周围介质的温度。

06—马赫数（Ma）

流体力学中表征流体可压缩程度的一个无量纲参数，记为Ma，定义为流场中某点的速度v同该点的当地声速c之比，

亚声速不可压缩流：M<0.3

亚声速可压缩流：0.3≤M≤0.8

跨声速流：0.8≤M≤1.2

超声速流：1.2≤M≤5

高超声速流：M≥5

微信公众号：“CFD流”

关注我，我有一万个CFD故事讲给你听

注：以上内容来自传热学、流体力学及百度百科等。