CHAID 响应模型与市场细分

Tony Babinec

    作者简介： Tony Babinec 是 SPSS 公司的一位市场经理。 SPSS 公司是一个开发并推广市场研究分析软件的公司。

    研究中一种很常见的情况是需要使用一组解释变量来预测一个响应变量。当分析中的大多数变量（包括响应变量在内）为数值型时，研究者多采用多元回归的方法进行分析。然而，市场研究人员常常需要处理其值为类别型的种类变量。

预测一个交叉状响应

    响应变量在通常情况下都是交叉的。例如：

    · 一个直销商投递出 20 ， 000 份邮件，收到了 500 份回复。用什么标准将回复人与未回复人区分开？

    · 征兵办公室给两年兵役期满的士兵提供重新入伍的机会。用什么标准将重新入伍者与不重新入伍者区分开？

    · 某大学招生办想要确保招生定额。用什么标准将接受录取的学生与不接受录取的学生区分开？

    在以上的每个例子中，响应变量都是交叉的。

    在实践中，研究者有时会将多元回归技术应用于交叉响应模型。但是，当遇到交叉响应变量时，单纯的使用多元回归是不恰当的。这是因为此时多元回归所要求的假设条件不能得到满足。

    回归假设之一是残差具有一致性，如果因变量是交叉的，那么该假设就不能得到满足。

    回归假设之二是残差服从正态分布，如果因变量是交叉的，那么该假设也不能得到满足。

    回归假设之三是用回归方法所得到的预测值在一定程度上近似等于响应变量的真值。为了方便起见，我们规定响应变量的取值为 0 或 1 （据此将观测对象分为两个组：组 0 和组 1 ），进而希望预测值落入（ 0 ， 1 ）区间，预测值接近 0 表明该预测对象应归入组 0 ，预测值接近 1 表明该预测对象应归入组 1 。

    但是，回归的预测值并不是有限的，因此我们不能保证它一定落入 0 ， 1 区间。

    当一个响应类包含了大部分的响应时，我们称该响应变量是歪斜的。响应变量歪斜会使上述问题变得更为棘手。比如，在直销过程中，一次成功的邮寄应该达到 2-3% 的响应率，也就是说，直销商每寄出 100 份邮件，应该得到 2 至 3 份回应。在这个例子中，我们应该放弃多元回归而选择其他更适合的方法。

    有些研究者在响应变量歪斜时采用判别分析。判别分析适用于响应变量己被划分为两个或更多类别且解释变量是定量变量的情况。我们可以利用判别分析来确定使用哪些解释变量，采用什么样的权重来区分不同组的成员。但是，判别分析并不是一种理想的预测方法，而且当响应变量仅分为两类时，判别分析和多元回归分析在形式上具有一致性。在这种情况下，回归分析的缺陷在判别分析中同样存在。

    以前的 AID 和 SEARCH 程序同样落入了回归分析的框架中。虽然在实践中人们常用这两种方法处理交叉响应变量，但他们是为研究定量响应变量而设计的。回归分析的缺陷在这两种分析中也同样存在。

关于类别变量预测

    当解释变量也是分类变量时，回归分析和判别分析就更不适用了。但是这种情况市场分析人员和调研人员却经常遇到。他们需要使用地区、邮政分区、性别、种族等变量来预测一个分类的响应变量。

    针对分析中涉及的绝大多数或全部变量都是分类变量的情况，统计学家研究出一些方法，如 logistic 回归、 logit 分析等。虽然这些方法具有一定的适用性，但是他们往往过于复杂，分析出的结果也难于解释。幸运的是，在线性分析家族中存在一种简单易行的方法，它可以很直观地得出具有吸引力的结果，且在统计上具有有效性，它就是 CHAID 分析。

CHAID 分析的优点

    CHAID 代表着卡方的自动交叉检验。“卡方”是在分类模型中应用的一个统计量；“交互作用”是指进行成功预测所需要考虑的各变量之间的相互关系；“检验”是研究者想要完成的工作；“自动”则意味着这项指导性技术是可用的。下文中列举了一些在响应模型中应用 CHAID 的好处。

    研究人员通常会搜集大量的预期解释变量。 CHILD 可以用来提前筛选数据以剔除随机变量（对预测没有贡献的变量）。另外，对于那些已进入 CHILD 的变量，其进入的次序揭示了他们对预测的重要程度。

    一个分类变量包含着若干类别，但对响应变量而言并不是每一个类别都实际显著。 CHILD 可以帮助解决哪些类别需要合并的问题。比如，一组数据分为十二类，分别代表不同的地区，但是也许这 12 个类别仅有 3 种不同的响应模式。在这种情况下，应该合并地区分类。 CHAID 将进行统计检验，合并不显著的类别。

    有些解释变量可能由无序类别组成，有些则可能由有序类别组成。如果统计上可行的话，研究人员希望合并前者中所有的无序类别，而仅合并后者中临近的类别。 CHAID 可以实现这两种合并。

    回归分析适用于揭示线性关系。例如，假设随着受访者受教育程度的增加，针对相应问题回答“是”的百分比也增加了。那么这种模式就是线性的，回归分析可以揭示出这种关系。但是，如果随着受教育程度的增加，针对相应问题回答“是”的百分比是先增加后下 降的，那么，单纯的运用回归分析就无法揭示应答与教育水平之间的显著关系了，因为这个模式不是线性的。换句话说， CHAID 揭示非线性关系。

    回归分析揭示出主要的影响因素。也就是说，我们做回归分析时假设某个解释变量的影响相对于其他解释变量的取值而言是不变的。但事实未必如此。因此，研究人员在确定某一个解释变量对响应变量的影响之前，需要指定其他解释变量的水平。这被称为一个“指定影响” 或一个“交互作用”。 CHAID 能够揭示解释变量间的交互作用。

    CHAID 会生成一个分类树。研究人员可以从该分类树上找到统计上显著的分割点。由于 CHAID 在内置统计检验中运用了 Bonferroni 调节，这种基于一组数据构建的分割模型在一个类似的抽样样本中可以得到很好的交叉验证。

一个例子

    为了论证 CHAID 方法，我们从 1984 年的综合社会调查（国家舆论研究中心执行的一个关于美国成年人口的综合调查）中选取一些变量。这里的响应变量是反对人流（鉴于人工流产严重的危及孕妇的身体健康）。在这个样本中， 10.6% 的受访者反对人流，其余的 89.4% 支持人流。可能的预测指标包括：

    · 年龄段 共 3 组（ 18-32 岁， 33-52 岁， 53-89 岁）

    · 参加教会活动情况 共 9 类（从不参加过教会活动到每周参加一次以上教会活动）

    · 孩子的数目 共 9 类（从没有小孩到有八个或更多小孩）

    · 受教育水平 共 3 类（高中以下，高中，高中以上）

    · 婚姻状况 共 5 类

    · 种族 共 3 类（白色人种，黑色人种，其他人种）

    · 性别 共 2 类（男、女）

    在该分析中，参加教会活动情况的分类是单调的，如果统计上可行的话，只有临近的类可以合并。其他变量则被看成是“自由”变量，当统计上可行时，任何类别都可以合并。

    以下是 CHAID 分析生成的分类树形图：

   

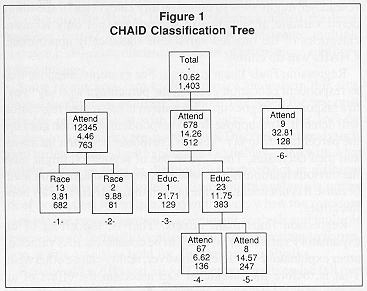
    从分类图上我们可以看到，参加教会活动情况（ attend ）是最重要的预测指标。根据这个指标，类别 1 到 5 被合并，类别 6 到 8 被合并，类别 9 单独作为一类。 CHAID 的一个重要的特性是，它不受二元分割的限制，这是其他 AID 方法所不具备的。在这里， CHAID 把参加教会活动情况分为 3 组。我们注意到响应变量的值随着组的变化呈现出增长的趋势：在孕妇的身体健康将受到严重威胁的情况下，很少参加教会活动的受访者反对人流的比率是 4.46% ；经常参加教会活动（每周一次）的受访者反对人流的比率是 14.26% ；频繁参加教会活动（每周一次以上）的受访者反对人流的比率是 32.81% 。

    聚类树的下一个分割点反映了一种交叉影响。即，如果受访者是一个很少参加教会活动的人，那么他的种族就是下一个最重要的预测指标；如果受访者是一个经常或频繁参加教会活动的人，那么他的受教育水平就是下一个最重要的预测指标。当种族是预测指标时，“白色人种”和“其他人种”就可以不再区分了，他们对响应变量而言是统计上不显著的。他们仅与“黑色人种”相区别。当受教育水平是预测指标时，“高中”和“高中以上”这两类是可以合并的，他们对响应变量而言也是统计上不显著的。他们只与高中以下的教育水平相区别。

    最后， CHAID 将“参加教会活动”变量中的第六、七类与第八类分开。

    总的来说， CHAID 分割分析将数据分为六组。根据响应的大小排序，分别是：

    每星期参加一次以上教会活动的受访者，反对人流的比率是 32.81 % 。高中以下文化程度，经常参加教会活动的受访者，反对人流的比率是 21.71% 。高中及以上文化程度，每周都参加教会活动的受访者，反对人流的比率是 14.57% 。很少参加教会活动，属黑色人种的受访者，反对人流的比率是 9.88% 。高中及以上文化程度，几乎每周都参加教会活动的受访者，反对人流的比率是 6.2% 。很少参加教会活动的白色及其他肤色的受访者，反对人流的比率是 3.81% 。

    说客、政治顾问和募捐者可以很好的利用这种分类来锁定活动针对的目标群体，或者避开那些“游手好闲”的人及持反对态度的人。

    让我们来看看 CHILD 分析都完成了哪些工作！如果有了上面的数据，大多数研究者都可以做一些粗略的分析，例如将变量两两组合制成交叉表并分析。从多元意义上讲， CHAID 分析输入的是一个 2*3*9*9*3*5*3*2 的表格。我们怎样搞清它的意思？ CHAID 分析揭示出重要变量，随机变量，交互作用以及可以合并的类。

    另外，对于那些经验丰富的分析师， CHAID 也可以提供用于构建正规模型的信息。分类树告诉我们哪些变量需要在进一步分析中加以应用，哪些变量应该舍弃。如果研究者对更为正规的模型感兴趣，那么，就需要对变量作记录以反映在 CHAID 分析中合并的类，然后根据表示影响的响应变量（ RESPONSE ） ，参加教会活动（ ATTEND ） 、种族（ RACE ） 、受教育水平（ EDUC ） 三个变量的主要影响，以及参加教会活动（ ATTEND ） 与种族（ RACE ） 、参加教会活动（ ATTEND ） 与受教育水平（ EDUC ） 的交互作用，借助 SPSS 中的 LOGLINEAR 构建一个 logit 模型。

结论

    CHAID 分析适用于人们通常都会遇到的分类数据。我们可以用一个交叉响应变量来说明 CHAID ，也可以用一个包含三、四个类别的响应变量来进行说明。 CHAID 是一种探索性的多元分析 技术 。它与对数线性模型同属一个技术家族。就像做回归分析一样，我们应该在分析中评价并选取重要变量以期得到有用的结果（而不必提及其正确性）。因为 CHAID 的输入数据是一个多维列表，所以采用大样本以期在 CHAID 分类树中获得详细说明是很有用的。也就是说， CHAID 应该是每一位研究者分析工具库中的一 件工具。