叶片的空气动力学基础

在风力机基础知识一节中介绍过叶片的升力与阻力基本知识，本节将进一步介绍相关理论知识。在风力机基础知识一节中已作介绍的不再重复，仅介绍有关内容的提高部分。

    常用叶片的翼型

图1是一幅常见翼型的几何参数图，该翼型的中弧线是一条向上弯曲的弧线，称这种翼型为不对称翼型或带弯度翼型。

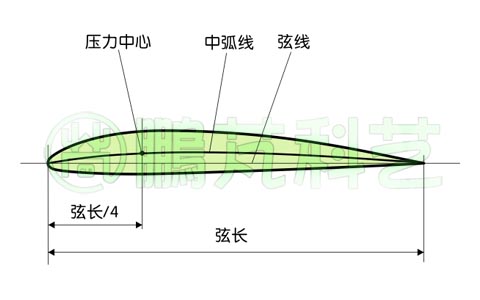
图1  翼型的几何参数

当弯度等于0时，中弧线与弦线重合，称这种翼型为对称翼型，图2是一个对称翼型。

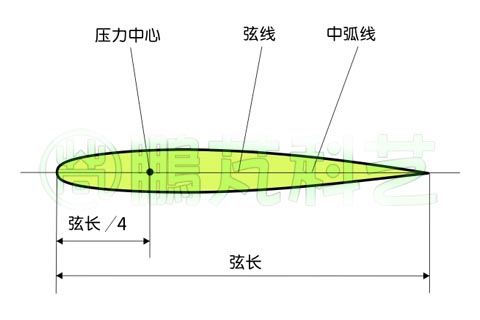
图2  对称翼型的几何参数

图3是一个性能较好的低阻翼型，是带弯度翼型，在水平轴风力机中应用较多。

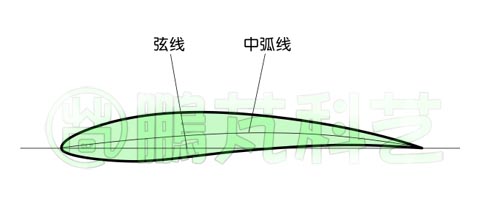
图3  带弯度的低阻翼型

    带弯度翼型的升力与失速

图4为一个低阻翼型的气流动力图，翼型弦线与气流方向的夹角（攻角）为α，正常运行时气流附着翼型表面流过，由于翼型与来流有攻角α，在靠近翼型上方的气流速度比下面的气流速度要快许多，根据流体力学的伯努利原理，翼型受到一个上升的力Fl，当然翼型也会受到气流的阻力Fd。

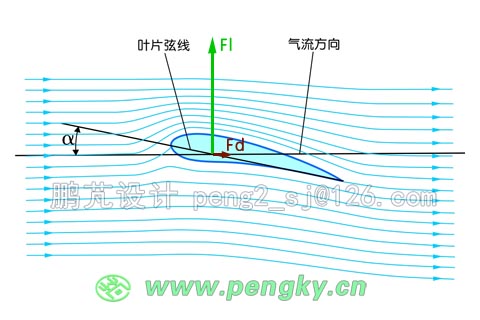
图4  翼型在来流下产生升力

这是正常的工作状态，有较大的升力且阻力很小，且升力随α增大而增大。但翼型并不是在任何情况下都能产生大的升力。如果攻角α大到一定程度，气体将不再附着翼型表面流过，在翼型上方气流会发生分离，翼型前缘后方会产生涡流，导致阻力急剧上升升力下降，这种情况称为失速，见图5

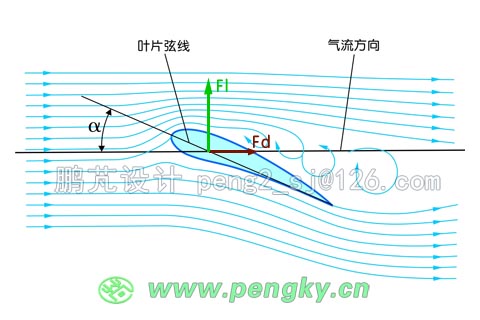
图5  翼型上方气流发生分离

翼型什么时候有最大升力，什么时候开始失速，通过翼型的升力系数与阻力系数随攻角的变化曲线图来表示，图6是这种翼型的曲线参考图，图中绿色的是升力曲线、棕色的是阻力曲线。在曲线中可看出，攻角α在11度以下时升力随α增大而增大，当攻角α大于11度时进入失速状态，升力骤然下降，阻力大幅上升，在α等于45度时升力与阻力基本相等。翼型开始失速的攻角α的值称为失速角。

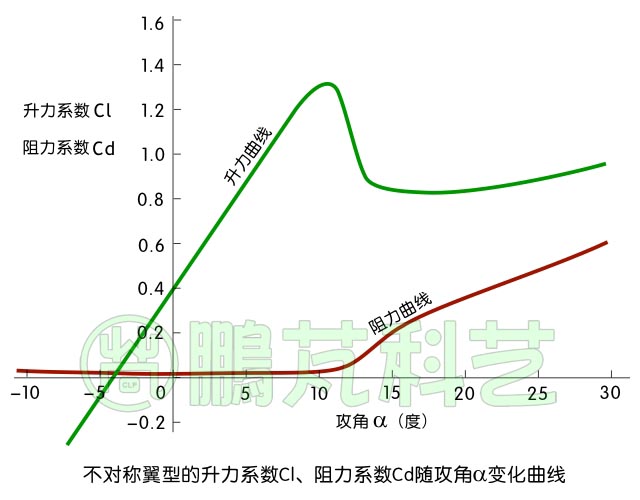
图6  有弯度翼型的升力阻力曲线

大多数有弯度的薄翼型与该曲线所示特性相近。在曲线图中看出翼型在攻角为0时依然有升力，这是因为即使攻角为0，翼型上方气流速度仍比下方快，故有升力，当攻角为一负值时，升力才为0，此时的攻角称为零升攻角或绝对零攻角。

翼型在失速前阻力是很小的，在近似计算中可忽略不计。

当攻角为0时，有弯度的翼型的压力中心在翼型的中部，随着攻角的增加（不大于失速角）压力中心向前移动到1/4弦长位置。

    对称翼型的升力与失速

对称翼型的升力与阻力等气动特性与有弯度翼型类似，但对称翼型在攻角为零时升力为零，因为此时翼型上面与下面气流速度相同。图7是对称翼型的升力系数与阻力系数随攻角的变化曲线参考图，图中绿色的是升力曲线、棕色的是阻力曲线。在升力型垂直轴风力机中较多使用对称翼型。

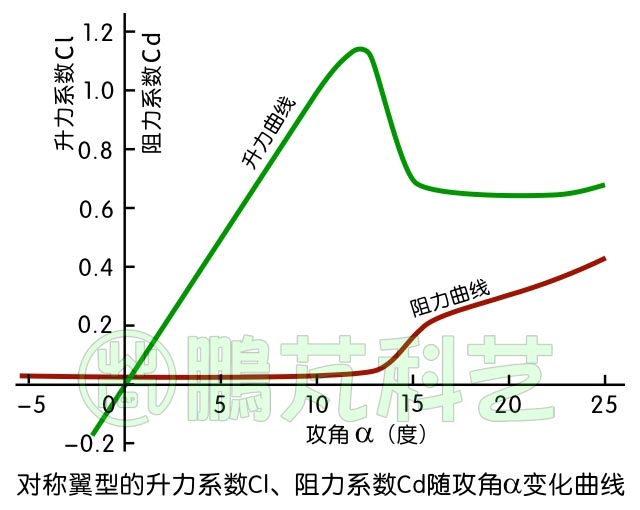
图7  对称翼型升力阻力曲线  

对称翼型的压力中心在不失速时在1/4弦长位置，不随攻角变化而移动，垂直轴风力机常用翼型是NACA0012与NACA0015，有关NACA0012的主要参数见NACA0012翼型的截面与升力曲线图一节。

比较有弯度的薄翼与对称翼型两个曲线图，两曲线相似，可近似认为在对称翼型中升力曲线经过0点，随着翼型弯度增加升力曲线向左方移动。

同时也近似认为在翼型失速前升力曲线的斜率是个常数，其值为0.1/度或5.73/弧度。

以上这些曲线都是在理想状态下的曲线，也就是翼型的雷诺数较大时的曲线。雷诺数小时最大升力系数会减小、失速攻角会减小、阻力系数也会增大，各种翼型在不同条件下的的升力系数要查阅相关翼型手册。

    叶片升力的计算示例

知道一个叶片的升力曲线，知道气体的流速与叶片的攻角就可以算出该叶片受到的升力，根据空气动力学，翼型在不失速状态下的升力计算公式如下：

Fl=0.5*ρ*Cl*v*v*c*l

   式中Fl 是升力，     单位是N（牛顿）
     ρ是空气密度，     在低海拔、常温下约为1.23kg/m3

Cl是升力系数

v是气体的流速，   单位是m/s

c是翼型弦长，     单位是m

l是叶片长度，     单位是m

计算示例1：

有一个低阻型叶片，长度为8m，宽度（弦长）为1m，空气流动速度是20m/s，攻角为8度，求其升力：

根据低阻型叶片曲线当攻角为8度时Cl为1.2，

Fl=0.5*ρ*Cl*v*v*c*l

Fl=0.5*1.23*1.2 *20*20*1*8=2361.6

计算出升力为2361.6牛顿

计算示例2：

有一个叶片为对称翼型，长度为8m，宽度（弦长）为1m，空气流动速度是25m/s，攻角为10度，求其升力：

对于对称翼型可根据攻角直接算出升力系数

Cl=10*0.1=1.0

Fl=0.5*ρ*Cl*v*v*c*l

Fl=0.5*1.23*1.0 *25*25*1*8=3075

计算出升力为3075牛顿