升力型垂直轴风力机的工作状态简析

在“达里厄风力机”一节中对升力型垂直轴风力机的工作原理已作介绍，鉴于目前国内对升力型垂直轴风力机作技术介绍的资料很少，本节通过近似计算对升力型垂直轴风力机的工作状态作简单分析，供大家参考，不对之处望大家指正，期待有更多的升力型垂直轴风力机资料供交流。

分析对象是一个“H”型垂直轴风力机，其叶片是固定的，取叶轮中一个叶片来分析，该叶片采用对称翼型，其弦长应远小于风轮半径。

翼型的叶尖速比与攻角

要使在气流中运行的翼型有最大的升力与较小的阻力，翼型必须有理想的攻角，水平轴风力机在风速与转速不变时其叶片的攻角也不变，而传统的达里厄风力机的叶片是固定的，也就是在风轮旋转一周时翼型自身也旋转360度，其攻角是在不停的变化。下面就是翼型旋转在4个象限时的攻角计算辅图。

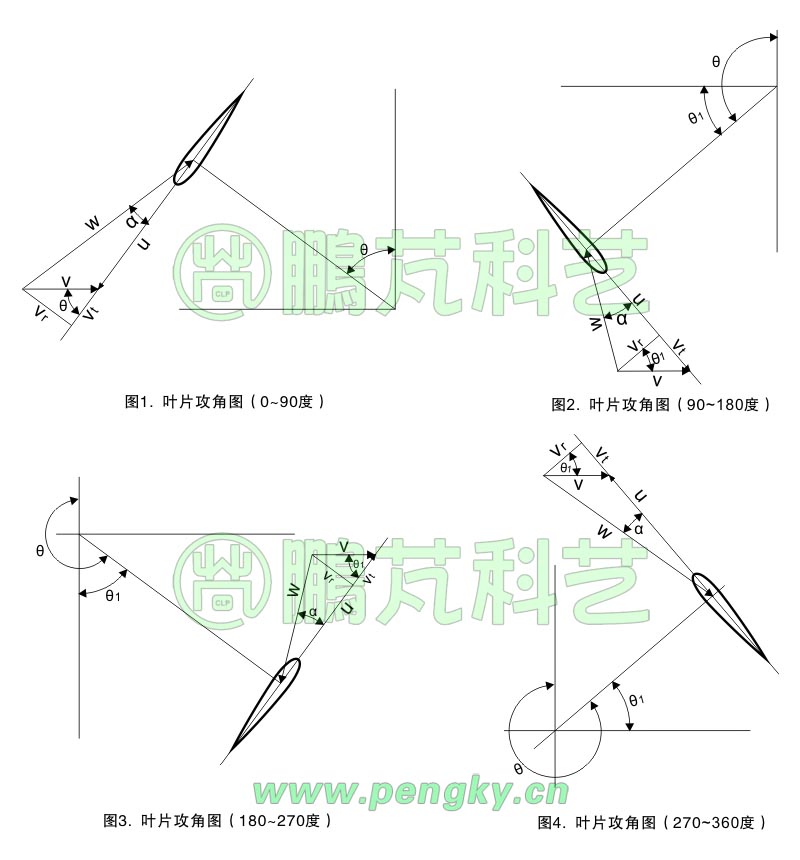
垂直轴风力机叶片在不同位置的攻角

为了便于观察分析，图中风轮半径缩小，攻角夸大。v是外来风速，u是叶片线速度， w是相对风速，α是攻角，θ是叶片绕风轮转角（叶片位置）。由于风力机由2个以上的叶片构成，在上风侧做过功的风速会降低，我们近似认为翼型在上风侧（0至180度）与下风侧（180至360度）的风向不变、但风能损失30%，下风侧风速降低至84%。

按图1来计算攻角

tanα=vr/(vt+u)

vr=v*sinθ

vt=v*cosθ

tanα=v*sinθ/(v*cosθ+u)=sinθ/(cosθ+u/v)    式中u/v是叶尖速比λ

α=arctan(sin(θ)/(cos(θ)+λ))            (1.1)     

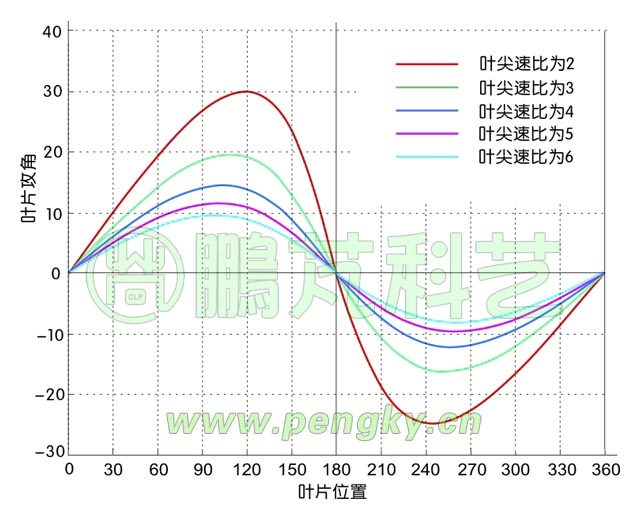
垂直轴风力机叶片的攻角变化曲线

图中每一根曲线显示了翼型在相应叶尖速比下的攻角变化，这个叶尖速比是按整个风轮计算的，实际上在下风面风速减慢，叶尖速比要比上风面大一些。

根据对称翼型的升力系数与攻角间的关系，失速角一般在11至13度（小翼型低风速可能不到10度），大尺寸翼型高风速状态下可达15度，所以翼型的最大攻角不要超过15度（小型机不要超过12度）。从以上图中可看出只有在叶尖速比大于4时，翼型的最大攻角才不超过15度。但叶尖速比也不能过大，过大使攻角过小而升力小，切向力更小，所以升力型垂直轴风力机的理想工作范围应该在4至6之间（小型机理想工作范围应该在5至6）。

翼型的相对风速

根据图1来计算相对风速，由于算式中“幂”不好表示，用“^”表示“幂”，^2是平方的意思。

w^2=vr^2+(vt+u)^2

vr=v*sinθ

vt=v*cosθ

w^2=(v*sinθ)^2+(v*cosθ+u)^2=v^2*(sinθ^2+(cosθ+u/v)^2)

w^2=v^2*((sinθ)^2+(cosθ+λ)^2)             (2.0)

w=v*√((sinθ)^2+(cosθ+λ)^2)              (2.1)

设外来风速v=8m/s，叶尖速比λ=4，用MATLAB软件计算翼型在一周中各位置的相对风速。在下图中将显示计算结果，图中下方蓝线是攻角变化曲线，上方绿线是对应的相对风速曲线，由于翼型在180度与360度位置时的风速v比8m/s略小，故对上述相对风速曲线略作修整。

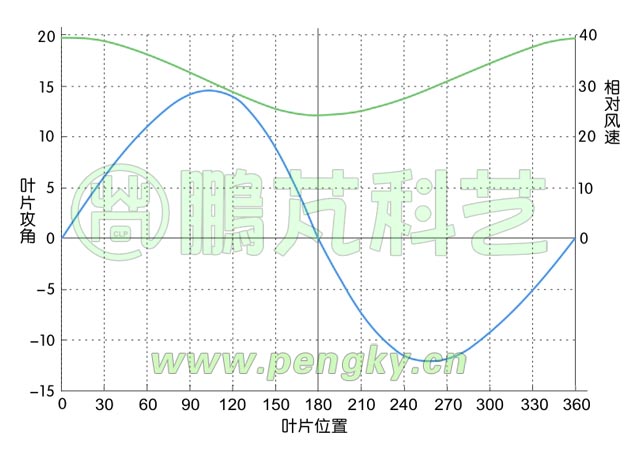
垂直轴风力机叶片的相对风速变化曲线

从图中看到叶片在0度时的相对风速最大，在180度时的相对风速最小。攻角与相对风速决定升力的大小，在下面将计算各位置的升力的切向力大小。

翼型的切向力

翼型的切向力是指翼型的升力与阻力在翼型旋转圆周上的切线方向的力，是推动风轮旋转的力。下面是翼型在不同位置切向力的计算辅图，图中为清楚显示阻力而夸大阻力若干倍，攻角也有所扩大。

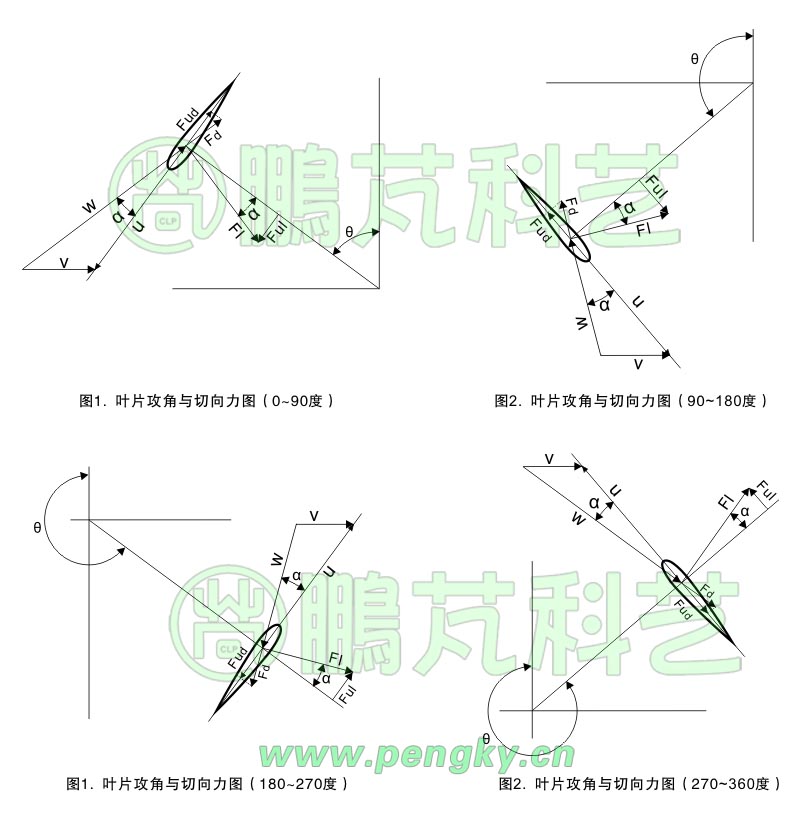
垂直轴风力机叶片在不同位置的切向力

图中v是外来风速，u是叶片线速度， w是相对风速，α是攻角，θ是叶片绕风轮转角（叶片位置）；Fl是升力， Ful是升力的切向力；Fd是阻力，Fud是阻力的切向力；Fu是升力与阻力的合成切向力。

根据图1来计算翼型的切向力，设定风速v=8m/s，叶片线速度u=32m/s，叶尖速比为4；设定叶片宽0.5m，长4m；攻角α的单位是弧度。

图中v是外来风速，u是叶片线速度， w是相对风速，α是攻角，θ是叶片绕风轮转角（叶片位置）；Fl是升力， Ful是升力的切向力；Fd是阻力，Fud是阻力的切向力；Fu是升力与阻力的合成切向力。

根据图1来计算翼型的切向力，设定风速v=8m/s，叶片线速度u=32m/s，叶尖速比为4；设定叶片宽0.5m，长4m；攻角α的单位是弧度。
升力系数 Cl=5.73*α，   阻力系数Cd=0.03，   ρ=1.2

升力系数 Cl=5.73*α，   阻力系数Cd=0.03，   ρ=1.2

Fl=0.5*ρ*w^2*Cl*0.5*4=ρ*w^2*Cl=1.2*w^2*Cl=6.88*w^2*α

Ful=Fl*sinα=6.88*w^2*α*sinα

Fd=0.5*ρ*w^2*Cd*0.5*4=1.2*w^2*Cd=0.036*w^2

Fud=0.036*w^2*cosα

Fu=Ful-Fud=6.88*w^2*α*sinα-0.036*w^2*cosα

Fu =w^2(6.88*α*sinα-0.036*cosα)              (3.1)

根据

α=atan(sin(θ)/(cos(θ)+λ))                  (1.1)

w=v*√(sinθ^2+(cosθ+λ)^2)                  (2.1)   

由于是对称翼型，正攻角与负攻角产生的升力大小是相同的，只是方向相反而已。用MATLAB软件进行对上面3式进行计算，得到翼型在0至360度位置的切向力曲线。

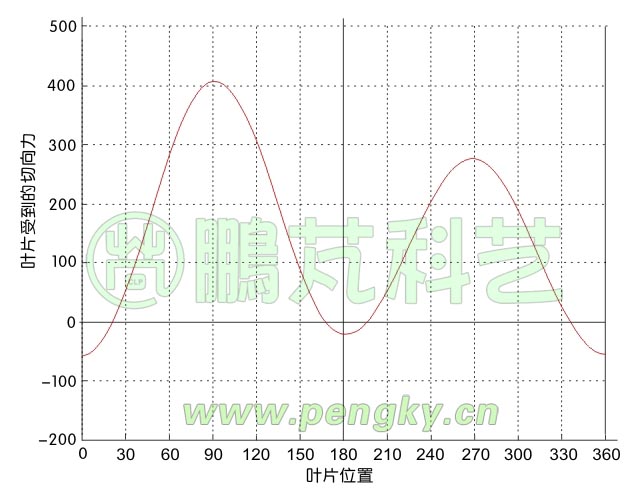
垂直轴风力机叶片的切向力变化曲线

从以上曲线看出即使是稳定的来风、均匀的转速，翼型在不同的位置产生的切向力也是不同的，在90度与270度附近最大，在0度与180度附近是反向力，这与水平轴风力机也是大不相同的。叶片在旋转中要受到正反两面的作用力，有可能引起共振，也造成叶片与风力机的疲劳，这是设计叶片与风力机的机械强度时要考虑的。

变化的切向力会影响旋转的均匀性，要想获得较均匀的旋转要有多一些的叶片，但多叶片也不一定是好事，一般3至5个较合适。下面就是3个叶片切向力的合成图，红、绿、蓝三根曲线是3个叶片各自的切向力，紫色为3个叶片合成的切向力。

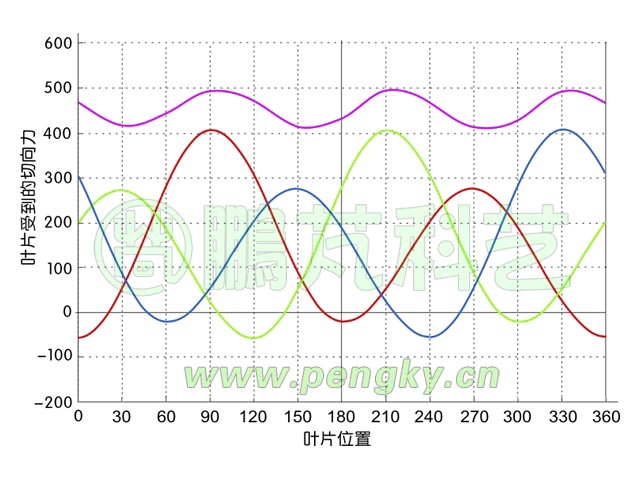
3个叶片垂直轴风力机的合成切向力变化曲线