|
人人都会流体力学——三、层流与湍流(2)
作者:佚名 转贴自:https://zhuanlan.zhihu.com/p/150407848 点击数:84
人人都会流体力学——三、层流与湍流(2) 汪键是个大胖子 中国科学技术大学 核能科学与工程博士在读 汪键是个大胖子 中国科学技术大学 核能科学与工程博士在读
好久没更新,首先跟各位读者说声不好意思,确实是忙加懒。 上次给读者们留了一个尖锐的问题。 根据伯努利原理,如果是理想流体的话,在管道内的任何一个横断面,液体的能量恒定,但是对于黏性流体,因为吸管内壁上黏性力的作用方向与流向相反,所以流速减慢。如下图:  综上所述,吸管内的流体越靠近嘴边,平均流速U就会越小,越慢。  根据连续性方程,吸管内流体的流动无论在哪个横断面上,其平均流速都是一定的。 首先我们先明确流动的上流和下流。 针对于吸管来说,因为饮料是从杯子里向嘴边流动,我们根据流动的方向,将靠近嘴边的叫做“下流”,而远离嘴边的叫做“上流”。 所以我们留的问题就可以用一个图来描述:  在我们的想象中,确实应该是这个样子的,由于黏性力的作用与流动方向相反,所以应该是对流动的速度会起到阻滞的作用,所以必然会导致从上流到下流的流动速度减小。 可是现在明确的告诉大家,实际的情况应该是这个样子的:  那么是为什么呢? 先说结论,因为还存在着一个力,能与黏性切应力保持平衡,从而使流体能够保证以相等的速度从上流到下流。 这个力在哪里呢? 在嘴里。 用吸管吸饮料,当你吸气的时候,意味着嘴里的压强是要低于大气压的,那么我们比较一下吸管上流出和下流出的压强大小。 很明显,跟上流处的压强p1相比,下流处的压强p2要低一些。  上流处从某种意义上来说我们可以认为是接近大气压的,而越靠近下流处也就是越靠近嘴的地方,压强就会越低,所以饮料会从压强高的上流处流到压强低的下流。 上流和下流压强差的存在,从而产生了“起因于压强差的应力”。 正是这个“起因于压强差的应力”,能和黏性切应力保持平衡。 解决了上篇文章里的遗留问题,现在继续说黏度和流量之间的关系。 流量这个概念其实大家见得都比较多了,针对于同样的吸管喝饮料的示例来说,流量就是在单位时间1秒钟内,有多少饮料流进了你的嘴巴里。 那么流量和黏度有什么关系呢?我们想象一下一个场景,在沙漠里,如果你现在嗓子已经干的快要冒烟了,甚至到了濒死的状态,现在有两杯饮品突然出现在你的眼前,一杯是浓浓的奶昔,另外一杯是乌龙茶,你会选择什么? 当然是选择乌龙茶了,因为它黏度低,可以在单位时间喝的更多,更能解渴。 所以流体的黏度越低,单位时间喝进的量就越多,也就是流量越大。 一根半径为r0的吸管,一秒钟可以吸入饮料的量Q有以下公式: 公式里的各项都很明确:r0是吸管的半径,μ就是流体的黏度, 很明显,流体黏度高的话,μ就大,所以相应的Q就会变小。 当然这个公式适用于黏度比较大的液体,如果是黏度比较小比较清爽的液体,流动的情况会涉及到湍流,会更复杂。 前面我们已经讲了流体的流速,流量,下面讲最后一个,能量。 黏性流体中,由于黏性切应力的作用方向和流体的流动方向是相反的,所以越接近下流处的流体能量损失就会越大,前面说过,在任何横截面的流体平均流速是恒定的,所以动能是不变的。 但是流体的能量E都在不停的损失着。 这种损失我们叫做“摩擦损失”,是由于黏性切应力而引起的能量损失。 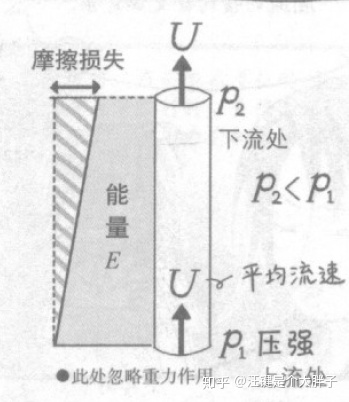 那么这部分流体流动中损失的能量究竟有多少呢? 首先,如果是没有黏性的理想流体,根据前面所说的伯努利定理,流体的能量沿着流线是恒定不变的。 但是黏性流体中,由于黏性切应力的作用,能量会损失,伯努利方程中所表示的能量E越靠近下流处损失的越大! 所以,针对于黏性流体,管道内某横截面的伯努利方程应该形式上有所变化: 这个公式就是“管流伯努利方程”。 和理想流体的伯努利方程有什么区别呢? 黏性流体的伯努利方程等式右边的能量E不再是一个常数,而是随着流线s不断变化,E是s的函数。  如上图所示,相距l的两个横截面之间,其损失的能量为 1、与管道长度l成正比; 2、与平均流速U的二次方成正比; 3、与管道直径d成正比。 千呼万唤始出来: 这个公式就是表示管道内摩擦损失的“达西-魏斯巴赫公式”!其中, 所以根据上面公式来说,如果用很细很细,并且长度非常长的吸管来喝饮料的话,那么管道摩擦损失的能量就会非常大,所以这个时候就很难喝到饮料。如果供给的能量小于管道内的摩擦损失,那么流体就不会流动。 当然上面说的情况都是直管,我们生活中见到的用到的很多管道就不是直管,是弯管。 管道的入口附近,弯曲的部分,以及横断面积突然增大或者减小的部分,都会产生流体能量的损失,这种损失我们叫做“压强损失”。 管道摩擦损失之外的压强损失一般用 其中, 至于损失系数的具体大小,可以分以下几种情况来讨论: 1、入口损失采用管道从广阔的空间吸取流体的时候,管道入口周围的流体就会改变流向朝管道入口的方向流动,此时管道入口部分就会产生能量损失。 这个入口损失系数会因为入口大小的不同从而有很大的差异。 通常认为喇叭形状的管道入口能够最大的减小入口损失。其损失系数差不多为0.0006。  2、管道横截面积突然增大横断面积急剧增大的管道,因为流动面积急剧变宽,从而扩大的部分会产生涡旋,因此导致了很大的能量损失。  入口处的横断面积为 3、管道横截面积突然减小在横截面积突然缩小的管道中,流体面积会缩小,与下流的横断面积  用 4、弯曲管道弯管可以根据曲率分维曲管和弯头管两种,曲率大的管道称之为弯头管。因为弯曲管道内侧的流体被挤压到半径方向,所以管道内部会产生旋涡。  用d来表示管道的直径,用 |